I just finished Is God a Mathematician? by Mario Livio. (I got my B.S. in mathematics and studied it for a year in graduate school, so I've always found math fascinating.) Dr. Livio investigates what Eugene Wigner called the "unreasonable effectiveness of mathematics": Why is mathematics such a powerful and effective tool for describing and predicting nature?

I have no idea why--I just think math is really cool. In fact, mathematics helps me describe and understand my faith.

For example, consider the idea of the fall from grace, as described in Genesis 3. This story explains humanity's sinfulness. (Unfortunately, too it's easy to become too obsessed with human sinfulness. We're sinners. Now let's move on.) We seem to have forgotten the first part of the story, as told in Genesis 2: Human beings first lived in a state of original innocence. Saint John Paul II connects these two states--original innocence and original sinfulness--in his Theology of the Body:

As an expression and symbol of the covenant with God broken in man's heart, the tree of the knowledge of good and evil delimits and contrasts two diametrically opposed situations and states: that of original innocence and that of original sin, and at the same time man's hereditary sinfulness which derives from it. (Pope John Paul II, General Audience of 9/26/1979)

In other words, the tree of knowledge of good and evil is an inflection point.

In the mathematics, an inflection point is a point on a curve at which the sign of the curvature changes. That is, the curve goes from being concave (opens up) to convex (opens down):

In the graph to the right, the point (0,0) is the inflection point--notice how the graph opens up--it is concave--to the left of the point (0,0) and opens down--it is convex--to the right of the curve.

Prior to eating from the tree of knowledge of good and evil, humanity lived in a state of original innocence. (Think of this as the concave part of the graph above.) Afterward, we lived in a state of original sinfulness. (Think of this as the convex part of the graph above.)

Notice that in the above graph, original sin never takes away our original innocence--they are part of a single, continuous curve.

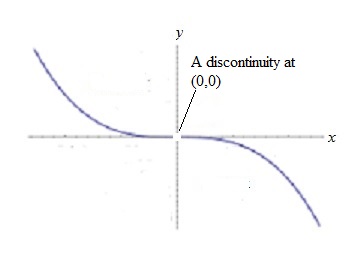
But sometimes, instead of treating original sin--that is, the result of the sin of Adam and Eve (see Genesis 3:6)--as an inflection point, we treat it as a discontinuity:

In this graph, there is a discontinuity at the point (0,0). That is, the curve "breaks" at this point.

Notice the "hole" where the inflection point used to be? This totally changes the graph. The two sections of the curve are completely separate--if you were tracing this curve with a pencil, you cannot go from one section to another without lifting it up. In effect, instead of there being one curve, there are two. Our original innocence is completely separate from our original sinfulness. As long as we treat the fall from grace as a discontinuity, we will find it all too easy to live in a world where we will use labels like "saint" and "sinner" to divide us.

But John Paul II tells us that we cannot talk about original sin without first making reference to our original innocence:

However, Christ's words . . . enable us to find in man an essential continuity and a link between these two different states or dimensions of the human being. . . . It is impossible to understand the state of historical sinfulness without referring or appealing (and Christ appealed to it) to the state of original (in a certain sense, "prehistoric") and fundamental innocence. (Pope John Paul II, General Audience of 9/26/1979)

In his ministry, Christ not only appealed to that fundamental innocence, he completed the curve by removing that discontinuity altogether. What was once two--one concave curve and one convex curve--now become one continuous curve. We see this continuity when we hear the tax collector pray, "O God, be merciful to me, a sinner." (Luke 13:18) He recognized his sinfulness, but by trusting in God's infinite mercy, he found his original innocence. We see this continuity when we celebrate the sacraments, especially the Eucharist. And we see this continuity when we find God in all things.

Of course God is not a mathematician; but both God and mathematics are beautiful and wonderful to behold. And God uses mathematics--as God uses all things--to help me grow in faith, hope, and love.